Look, sometimes the “no pain no gain” route is the best way. Want to climb Everest? Not many shortcuts there, unless you’re someone who has the money to commandeer a rocket to drop you (pretending to look haggard for the selfie) right on the summit. (And, honestly, don’t be that person.)
Obviously, raising your SAT score will take time and effort. But because students ask a lot, this guide is all about finding the most efficient ways to raise your score in the least amount of time. Is this a comprehensive study plan? It is not.
Will it provide 1 strategy + 1 skill in each section of the test pretty much GUARANTEED to lead to a score boost? You bet.
READING
The Strategy: Active Reading
Here’s a great way NOT to absorb what you read: sit way back in your chair, pencil down, and just try to let the passage wash over you like a word shower.
Sure, it may be a relaxing way to read, but it’s definitely not effective, kinda like how you’d never see a detective go through a crime scene just kinda “vibin’ it out.” What would an effective detective do instead? We’ve all seen the scene: first they don the latex gloves, then they pick stuff up, open drawers, and look more closely at anything and everything of interest.
That is the image you want to emulate when you read an SAT passage. You don’t need (and don’t really have the time) to be as thorough as our hardboiled detective, but you do want to be able to
quickly and confidently discern what information is most important in a given passage
find a way to indicate it visually in order to help yourself later when you’re answering questions.
Here are 3 ways to do that. Rarely is reading one size fits all, so play around with these (as well as any of your own ideas) until you find a system that works best for you. Just make sure you do some form of active reading on the SAT. It’ll help. I promise.
1. Pre-highlighting
My tutoring students often ask if they should read all the questions before they read the passage. To this I say no, primarily because that’s mostly a waste of time. The caveat, however, is for questions that have specific line references. I don’t advocate reading these questions so much as scanning the questions (all of them in 45 seconds max) for line references and then marking (or “pre-highlighting”) those lines in the text.
This gives students a visual clue when they come across a line or set of lines they know they will be asked about directly. Again, this process of scanning questions and marking lines should be done as soon as you begin a passage and should ideally take no more than 30-45 seconds. But it really sets you up well to quickly and effectively answer line-reference questions.
2. “Caveman” Notes
This strategy basically just means “little notes in the margin of a paragraph.” Why do we call them “caveman” notes? Because they’re the dumbest, shortest (2-5 words) version of a paragraph’s main idea. If you read ‘em out loud, you’d sound a bit like a Neanderthal (who technically had bigger brains than we do, but…).
Good examples of caveman notes: “desalination process = hard” or “Constitution good.”
3. Underlining/Circling Key Terms
I’m not re-inventing the wheel here—you’ve probably been doing some version of this in school since you were in 3rd grade (and if not, hey, great time to start). This is just a reminder to also do it on the SAT!
What kind of information is the most helpful to underline or circle?
Main ideas (i.e. topic or concluding sentences)
Big shifts (i.e. contrast words like “However,” “But,” or “Surprisingly”)
The introduction of a defined term, name, or number
Very + or very - POV words (especially on double passage)
Example: Here is a short passage containing some very + POV words
Not only did introducing a four day work week make the CEO beloved by her employees, allowing workers to maintain a better work/life balance actually led to greater productivity, leading to a noticeable increase in sales and a commensurate rise in stock price in addition to happier workers and lower employee turnover.
Example: And another containing clearly - POV words
As it stands, the proposed law is clearly unconstitutional because it would render null and void the basic right of citizenship to all those born on American land as guaranteed by the 14th Amendment; any proponent who argues otherwise either does not understand what the bill actually says (in which case he is a fool), or is attempting to hoodwink the American public into welcoming a Trojan horse into our democracy (in which case he has betrayed his oath of office.)
And why is it a good idea to underline/circle these things?
Well, first of all, the extra second it takes you to underline/circle actively tells your brain this is important, adding to the likelihood you’ll retain the information.
Also, since there’s just no way to retain all the important information in a passage upon initial reading, these markings will provide the kind of visual trail of breadcrumbs that will help you find it again quickly when answering the questions.
The Skill: Wrong Answer Traps
Picture again your version of the crime scene detective from before. Remind yourself that this is who you want to be when tackling the SAT reading section.
Why?
Because, unlike in an English class where nuances of meaning and multiple interpretations are the name of the game, the SAT is a multiple choice test! That means there can only be ONE RIGHT ANSWER per question.
Sayonara, nuance! Stay in your lane, multiple interpretations!
The only way to create a question with a single right answer (something the SAT has to do or everyone makes fun of them and calls them dumb) is to make the 3 other answers demonstrably wrong! Now, if they were all demonstrably, very obviously wrong, the questions would be too easy. So! They’ve got to make them demonstrably, yet subtly wrong, and that’s where you’re sleuthing skills come in.
The name of the game is “provability,” and any answer choice that is not 100% provable in the text is wrong. As always, it helps to know what to look for. Here are the 3 most common “wrong answer traps” on the SAT Reading Section.
1% wrong = 100% wrong
Here, the issue is that the answer choice looks so very very right. And for good reason! It IS so very very right … almost. Sometimes, the problem comes down to a single word! Let’s say a science passage answers how scientists set up a particular experiment but not why they set it up that way. An incorrect answer choice could be totally provable except for the word why.
Remember, it’s easier to dis-prove a single word in an answer choice than it is to prove every single word, so if you’re looking for ways to find fault with an answer choice, you’ll be likelier to notice these sneaky little buggers. Otherwise, it’s easy to talk yourself into answers that are actually wrong.
100% right … to a DIFFERENT QUESTION
These answers are tricky because they ARE 100% provable … if the question had asked you something just a little different. Let’s say a double passage asks you to choose a statement with which both authors would agree. Often, in cases like these, 1-2 wrong answer choices will be 100% provable statements that only one author would agree with. 100% provable? You betcha. Does it answer THIS question about both authors? Nope. Those answers would be wrong.
Out of Scope
These answers are wrong because they are either written too broadly, too narrowly, or in more extreme language than that which can be proven.
For example, let’s say a survey of 10 people showed that more than half of those surveyed believed climate change affects their lives personally. An “out of scope” answer might claim that, “most people on Earth believe climate change affects them personally.” Is that possibly true? Yes! Can we prove it from a survey of 10 random humans? Not even close. The answer choice is too broad, and therefore it is “out of scope.” In general, the more definitive wording an answer choice uses (“most” rather than “many,” “certain” rather than “it’s possible,”) the harder it is to prove, and therefore the more likely it is to be wrong.
Key takeaway: Notice that each of the three points above are tools for elimination. Again, the SAT has to make wrong answers clearly (if subtly) wrong (if it’s just their opinion that an answer is better, their test fails), so a useful reframe on the SAT Reading section is that you’re not looking for what’s right so much as you’re choosing whatever answer is left that you can’t eliminate.
WRITING & LANGUAGE
The Strategy: Keep it Short!
If you walk away from this blog remembering JUST ONE THING, it should be this: when it comes to answer choices on the SAT Writing & Language section, the fewer words the better! Why? They hate redundancy, passive voice (almost always wordier than the “active version” of the same thought), and over-punctuation (so “keep it short” also just generally means “less is more.”) So, when in doubt … take it out!
Example:
However, most high schools in the U.S. start by 8:30 or earlier, nearly guaranteeing that the entire student body of a given high school will arrive chronically sleep-deprived in a habitual way.
NO CHANGE
habitually.
Over the long term.
DELETE the underlined portion and end the sentence with a period.
The correct answer here is D. Why? Because I just told ya to keep it short, brah, and what’s shorter than taking out the whole underlined portion?! Also, what does “chronically” mean? Well, it means …”happening repeatedly over time.” What does habitual/habitually/over the long term mean? Same. Exact. Thing.
Note: The “keep it short” rule applies predominately to grammar questions (as in there’s no question stem, just answer choices). If a question stem asks you to do a specific job (Ex: “Which choice most specifically supports the main idea of the sentence” etc.), IGNORE THE “KEEP IT SHORT’ RULE. Focus exclusively on the specific job at hand.
The Skill: All Things Comma
The SAT is crazy for comma questions. If commas were llamas, the SAT would open a petting zoo. If commas wore pajamas, the SAT would start a sleepwear company. If commas were from Yokahama … well, you get it.
The most basic rule when it comes to commas on the SAT is this: GET RID OF AS MANY COMMAS AS POSSIBLE. That said, there are times when we need to use a comma. Here are the four main rules for comma usage on the SAT.
1. Use a comma and a coordinating conjunction (fanboys) when linking two independent clauses.
Examples:
Maria went to the market to buy groceries, but she forgot to bring her shopping list.
— — —
Professor Thompson wanted to brush up on his knowledge of ancient languages, so during his vacation in Egypt he took a course in Aramaic at Cairo University.
2. Use a comma when a sentence starts with a dependent clause followed by an independent clause.
Examples:
Because my car had broken down, I jogged to work.
— — —
Although I am a pretty fast runner, I was still 10 minutes late to the morning meeting.
3. Use commas to separate either items in a list or multiple adjectives that each describe the same subject (and those adjectives could also be used in reverse order).
Examples:
I never had a mom, a dad, a dog, a friend, or a good night’s sleep.
— — —
My silent, happy sister simply nodded her head in amazement.
(Whereas “the charcoal gray sweater” should have no comma.)
Note: DO NOT place a comma between a single adjective and a two-word noun. For example, “the crumbling high school.” The word “high” can be used as an adjective, but here it is simply part of the noun. The “high school” is “crumbling.” The “school” is NOT both “crumbling” and “high”… unless maybe it’s on top of a mountain?
4. Use commas to bracket off “unnecessary information”
By “unnecessary information,” we mean phrases or clauses (or words) that could be removed from the sentence without destroying the integrity of the sentence structure.
Examples:
The Statue of Liberty, which sits in New York Harbor, is a cherished symbol of freedom.
— — —
Ben took a trip to New Orleans, the birthplace of jazz, to celebrate his graduation from music school.
Note: DO NOT place commas around information that, if removed, would harm the structural integrity of the sentence. You may see this most often in sentences including proper names.
Example:
Immunologist Anthony Fauci recently retired from his role as head of the federal government’s COVID response taskforce.
It’s tempting to want to put commas around the name Anthony Fauci. Sometimes we think we have to do this … but here, we don’t and shouldn’t! And look what would happen if did! Take it out, and the sentence reads, “Immunologist recently retired from…” Nope. That sentence just lost its subject!
MATH
The Strategy: Plugging-In
Let’s face it: ya gotta know some math to ace the SAT math section. However! There are strategies that can help us sneak in a side door when that metaphorical mathematical “front door” remains locked to us, whatever the reason (forgot the concept, never learned the concept, fatigue or anxiety is prohibiting your brain from seeing the obvious, etc.).
Never fear! (Dramatic fanfare plays.) Plugging-In is here!
This strategy allows students to simply replace variables or vagaries with real numbers (that students make up according to rules/limits described), and solve the problem that way. Essentially, the fewer specifics the question provides, the more power YOU have to fill in those specifics in order to simplify and solve with less conceptual rigamarole.
How does “plugging in” work?
STEP 1: “Make up” your numbers, making sure to follow any rules or limitations outlined in the question. For example, if the question states that “x is an integer greater than 3,” you need to choose a whole number greater than 3 (so … maybe 4!). If you notice in the question that you’ll eventually have to divide your number by 5, go ahead and make up a number that you know is divisible by 5. You don’t have to, but it will make your life a whole lot easier.
STEP 2: Solve the question with your numbers to find your “target answer.”
STEP 3: Re-plug in your original number(s) into the answer choices to find which answer choice “answer” matched your “target answer.”
Let’s try one, shall we?
Example:
The circus is coming to town! It costs x dollars to see the elephants and half of that amount to see the monkeys. If n people in a group buy tickets to see both attractions, what will the total cost for the group be in terms of x and n?
A) x(n + ½)
B) 3n/2x
C) 3nx/2
D) nx/2
Now, is there a purely algebraic way to solve this question! You bet! And if that method feels more intuitive to you, go for it! However, if you’re looking at all those variables like … NOPE … plugging in might be the best strategy for you.
STEP 1: Make up a number for x, knowing you’re going to need to divide it in half to get the cost of the monkey attraction. So, an even number is probably best. Let’s say x = 6.
STEP 2: So it’s $6 to see the elephants, which means it’ll cost you $3 to see the monkeys, and $9 to see both attractions. Now, let’s see if there are any restrictions/rules about what “n” can be … and there aren’t, so you can really make it whatever. (NOTE: As a rule, it’s a good idea to stay away from using “O” and “1” as plug-in numbers because they behave in ways other numbers do not.) So, how about 2? If n=2, it’s going to cost $18 total for 2 people to see both attractions. Therefore , $18 is our target answer!
STEP 3: Now start plugging in x (6) and n (2) into the answer choices until you find an answer that ALSO = $18. And the winner is … C.
The Skill: The Algebra “Big 7”
The SAT Math section is algebra-heavy. VERY algebra-heavy. In fact, of the 20 questions on a given No Calculator section, 18 or so of these questions are usually algebra.
Not only that! While these questions do require foundational knowledge of algebraic concepts (order of operations, exponent rules, etc.), they almost all fall into 1 of 7 categories related to what you’re actually supposed to do.
The better you become at recognizing which of these 7 things is required in a given question, the easier and faster you’ll be able to answer it. I give you … drumroll please … the Algebra “Big 7!” (With answers below, so you can try them yourself and check.)
1. Set-up
These questions generally contain a word problem followed by answer choices which are simply different ways to “set up” the information given in the word problem. Here, you don’t have to solve anything! You just have to know how to rewrite the word problem into an expression or equation.
Example:
Amy and Oscar recorded the number of miles eachof them walked. Amy walked n miles each day for 12 days. Oscar walked 4 miles more each day than Amy walked each day. If Oscar walked for t days, which of the following represents the total number of miles that Oscar walked?
A) n + 4t
B) t(n + 4)
C) n(t + 4)
D) 4n + 16t
2. Solve
Here, the test-makers have already set up the algebraic equation. It’ll be front and center in the question. You just have to solve!
Example:
If 3(x – 7) = t and t = 9 , what is the value of x?
A) -10
B) -4
C) 3
D) 10
3. Set-up AND solve
Now let’s put #1 & #2 together! You’ll again see a word problem requiring you to set up an algebraic equation, only this time you’ll need to go the extra step and solve it as well.
Example:
A toll bridge in Florida charges $0.75 for each car and $1.10 for each truck crossing the bridge. During a 24-hour period, a total of $326.55 was collected for tolls. The total number of vehicles that paid a toll was 399. How many trucks crossed the bridge that day?
A) 78
B) 148
C) 176
D) 297
4. Move around
Much as in #1, the answer choices will all simply be different versions of the same algebraic expression or equation. Generally, this is also accompanied by an existing equation in the question stem. For these questions, you’ll notice that the answers will simply be the same equation solved for a different variable. Your job? Just “move around” (read: order of operations) the original equation until you’ve written it in terms of the new variable. No solving required! You’re just rearranging individual pieces to make a new picture with the same images. Or, to put it another way, creating a slightly different dish using the same ingredients.
Example:
S = πrl + πr 2
The formula above gives the total surface area, S, of a cone whose base has a radius of r and a slant height of l. Which of the following gives l in terms of r and s?
A) l = S/πr – r
B) l = S/πr + r
C) l = rS/π – r 3
D) l = S/π – r 2
5. Identify
Another one that’s deceptively easy once you figure out what’s going on! Again, you’ll be given a word problem. The question stem will describe a real-world scenario that can be written as an algebraic equation (hint: it’s almost always y= mx + b). However, instead of solving for anything, you’ll be asked what a piece of this algebraic equation represents in the equation. Well, if it’s y = mx + b (and again, it usually is), there are really 2 parts of this equation that mean something significant: m (slope) and b (y-intercept). Since slope represents a constant rate of change between each set of points, answers for m are usually something like, “the amount a customer pays per day for fuel.” Since y-intercept represents a fixed point (in real world scenarios, this is almost always the starting point), answers for b are usually something like, “the initial fee a customer pays for renting the jetpack.”
Example:
V = 48m + 650
Juan uses the equation above to estimate the value, V, of his savings account, in terms of the number of months, m, after he opened the account. What does the number 650 represent in this equation?
A) the value of the account after 1 year
B) the value of the account after 1 month
C) the dollar amount that the account increased by each month
D) the dollar amount that Juan deposited in the account when he opened the account
6. Systems of Equations
These questions will be visually apparent by the simple fact that you will be given TWO equations instead of 1. We will get more in-depth with a couple specific types of these questions in the video portion of this blog, but in general, you’ve got 2 ways to solve a system of equations: Substitution and Elimination.
Example:
x + y = -4
2x + y = 9
Using the system of equations shown above, what is the value of x ?
7. Linear v. Quadratic v. Exponential
If you decided to improve your SAT score by becoming a genius at 1 single concept, LINEAR EQUATIONS would be that concept!
Linear equations are so prevalent on the SAT, I got y = mx + b tattooed on my face. Okay, no I didn’t, but learn everything you can about y = mx + b as if you want that knowledge to be just as permanent as my non-tattoo!
However, QUADRATIC and EXPONENTIAL functions also come up a lot on this test too, so if you have the time and dedication to master all 3 of these concepts, you’d be doing yourself a great service. There’s enough content related to these 3 concepts to fill multiple blogs, but for the purposes of this brief review, here is one sample question each to begin your journey.
LINEAR:
This one’s a bonus! If you were paying attention, you may have noticed that Example Questions 3 (set up & solve), 5 (identify), and 6 (systems of equations) ALL dealt in some way with y = mx + b equations. However, since y = mx + b is so important on the SAT, here’s one more:
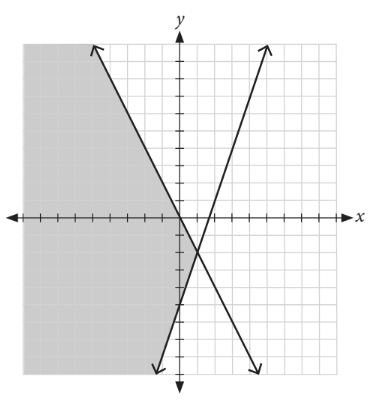
Example:
What is the system of inequalities that is graphed above?
A) y > -2x
y < 3x – 5
B) y < -2x
y < 3x – 5
C) y ≥ -2x
y ≥ 3x – 5
D) y ≤ -2x
y ≥ 3x – 5
QUADRATIC:
Example:
The function f(x) = 2x2 is translated 5 units to the left and 8 units down to create function g(x). Which of the following is the equation for g(x), in the form that reveals its x-intercepts?
A) g(x) = 2(x + 5)2– 8
B) g(x) = 2(x + 3)(x +7)
C) g(x) = 2x2+ 20x + 42
D) g(x) = 2(x2 + 10x + 21)
EXPONENTIAL:
Example:
The value of a new car depreciates at a rate of 15% per year. If C represents the cost of the car when it was new, which expression represents the value of the car t years after it was purchased?
A) 0.15Ct
B) 1.15Ct
C) C (0.85)t
D) C (1.15)t
Answers to the Algebra Big 7 examples above:
B
D
A
A
D
13
Linear: D
Quadratic: B
Exponential: C
Final Thoughts
Yes, the SAT can feel like a behemoth of a test. But take the time to really get down the strategies and skills above. With them, you won’t be taking a rocket to the top of Everest … but you’ll be giving yourself a quick lift from base camp. And that’s a huge boost in helping you get up past the Khumbu ice fall and … wow, we could really just keep running with this metaphor.
Special thanks to Martha Marion for writing this blog post.
Martha (she/her) is a teacher and performer from Los Angeles, California. She received her undergraduate degree from Northwestern University and is currently working towards an MA in Psychology from the University of the West. Martha has been tutoring since 2005, focusing on the SAT, ACT, U.S. History, and all things Language Arts. She is also an actor, director, and teaching artist with The Story Pirates, facilitating creative writing workshops all over Los Angeles and helping to adapt kids’ work for stage, screen, and podcast. When not working with students, you can hear Martha’s voice in video games such as God of War and Saints Row as well as animated programs such as the upcoming Transformers: Earthspark on Nickelodeon.